Diversión con pasatiempos geométricos en la playa

Ahora que estamos en verano, tenemos una buena ocasión para divertirnos con algo de geometría en la playa. Se pueden hacer unos castillos de arena geométricos muy bonitos, como nos lo demuestra también Calvin Seibert.

http://www.flickr.com/photos/45648531@N00/sets/72157594166672630/

Él los construye a lo largo de todo el año y suele combinar ingeniosamente diversas formas geométricas, pero también hace construcciones llamativas juntando únicamente paralelepípedos de arena bien compactos.

http://www.flickr.com/photos/45648531@N00/sets/72157594166672630/

Al observar estas construcciones o intentar construir unas similares, surgen muchas preguntas que requieren algo de ingenio y ayudan a activar las neuronas mientras uno se divierte. Algunas de ellas son, por ejemplo, estas cuatro:

ACERTIJO 1

Para empezar, pueden hacerse unas construcciones sencillas de arena formadas a partir de la colocación ingeniosa de 6 paralelepípedos de más o menos el mismo tamaño. La colocación tiene que cumplir unas condiciones a la vez que se considerará lo siguiente:

Un paralelepípedo se une a otro para formar otro paralelepípedo u otro cuerpo escalonado más grandes siempre que una cara o parte de la cara de un paralelepípedo entra en contacto con una cara o parte de una cara de otro paralelepípedo. Si se tocan únicamente en una esquina o arista, entonces se considera que los paralelepípedos en cuestión no se unen entresí formando un nuevo cuerpo.

Caso 1: ¿Cómo pueden disponerse 6 paralelepípedos para que cada uno de ellos se una con dos y sólo dos paralelepípedos?

Caso 2: ¿Cómo pueden disponerse 6 paralelepípedos para que cada uno de ellos se una con tres y sólo tres paralelepípedos?
Caso 3: ¿Cómo pueden disponerse 6 paralelepípedos para que cada uno de ellos se una con cuatro y sólo cuatro paralelepípedos?

ACERTIJO 2

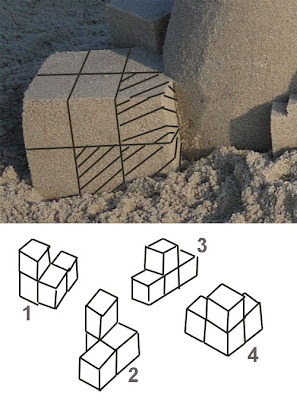
En la figura siguiente puede verse un paralelepípedo grande formado a partir de 6 paralelepípedos (cubos, si las aristas tienen todas la misma longitud) pequeños de arena. La pieza entramada de la esquina se construyó en primer lugar poniendo en contacto cuatro cubos de arena. Esta primera pieza puede haberse formado de 2 formas. ¿Cuáles son?

ACERTIJO  3

En los cuerpos platónicos se cumple una relación matemática entre número de esquinas E, número de caras C y número de aristas A.

Cuerpos platónicos

Esta relación se cumple de hecho también en otros cuerpos geométricos como, por ejemplo, paralelepípedos, prismas, pirámides, etc. 

¿Qué expresión matemática tiene esta relación entre esquinas, caras y aristas?
¿Se cumple también en un cuerpo con forma de escalera como el que se ilustra a continuación (o como en el que se puede ver en el castillo de arena de la primera fotografía)?

ACERTIJO 4

Se tienen únicamente dos cubos de plástico para coger y dosificar la arena necesaria: uno de tres litros y otro de cuatro litros. 

Sin embargo, se necesita disponer ahora de exactamente 1 litro de arena para construir un cubo de 10cm de arista. ¿Es posible conseguirlo con estos dos cubos? Y si es posible, ¿cómo?
Es decir, ¿qué habría que hacer para llegar a tener exactamente 1 litro de arena en uno de estos cubos de plástico?

(ver soluciones)

Física en la piscina

Aquí una pregunta de física diaria para estos días tan calurosos de agosto, en los que apetece nadar o estar muy cerca del agua:

Un grupo de niños y niñas está divirtiendose en la pequeña piscina casi circular de aproximadamente 5 metros de diámetro. Han puesto a flotar en ella un pequeño bote inflable, lo han llenado con 40 piedras pesadas, se han subido al bote y, tras muchas risas, han empezado a tirar las piedras en la piscina. Uno de ellos se quedó fuera de la piscina y se quedó todo sorprendido mirando la superficie del agua.

¿Porqué? ¿Cómo varía el nivel del agua?
¿Cuándo es más alto? Cuándo las piedras están en el bote o cuando están en el fondo de la piscina?

Si tras pensar en el efecto del desplazamiento de agua por bote, niños y piedras, en el principio de Arquímedes y el efecto del empuje, quieres comprobar también experimentalmente como se comporta el nivel, pero no quieres llenar la piscina con piedras o no tienes ninguna piscina pequeña a tu disposición, puedes hacer un experimento similar con un vaso (si es graduado, mejor) u otro recipiente lleno de agua (representan la piscina), un tapón de plástico suficientemente hondo para que no se llene de agua al cargarlo (representa el bote) y una, dos o tres monedas (representan las piedras más pesadas o densas que el agua).

¿Te ha sorprendido el resultado del experimento?
o ¿acertaste con la respuesta antes de realizar el experimento?

Aquí puedes encontrar unos cálculos que respaldan y explican lo observado.

Nota: esta pregunta de física diaria es un ejemplo de pregunta curiosa que plantean a veces los seleccionadores en una entrevista de trabajo para poner a prueba el ingenio y rapidez mental de los postulantes.