Casi cualquiera de nosotros a tenido la ocasión de haber jugado alguna vez al billar. Y seguro que lo que parecía fácil, eso de dar un golpe a una bola con un taco para que choque luego con otra, resultó ser mucho más difícil de lo esperado.
Sin embargo, hay algunas cuestiones sobre el billar que se pueden resolver geométrica y matemáticamente sobre el papel y que planteé en mi entrada de blog anterior. ¿Las has resuelto?
En la presente entrada de blog puedes encontrar una forma de resolver las cuestiones de tipo geométrico que no requieren la realización de ningún cálculo (grupo de cuestiones A). La resolución de las cuestiones matemáticas que requieren un cálculo (las del grupo B), podrás encontrarla en la siguiente entrada de blog.
Para situarnos, he aquí un breve resumen del problema a resolver:
Jan a Anna querían prepararse para su segundo encuentro de billar y analizar sobre papel el recorrido de una bola en unos casos sencillos, a fin de entrenar su sentido espacial y conseguir un buen ojo para la dirección de tiro.
Ya saben que la ley física que rige fundamentalmente el juego del billar es la ley de la reflexión, pero les falta resolver lo siguiente:
Grupo de cuestiones A: ¿Cómo puede encontrarse fácilmente, sin ir probando, la dirección de tiro adecuada en los tres siguientes casos de tiro sin efecto, tal como lo podría hacer mentalmente un jugador de billar?
 |
| Caso 1 - Tiro a una banda |
 |
| Caso 2 - Tiro a dos bandas |
 |
| Caso 3 - Tiro a 3 bandas |
¿La dificultad del tiro depende de la elección de las bandas? ¿El tiro a tres bandas es más fácil si se realiza golpeando la bola hacia la banda de abajo? ¿Porqué?
Un posible procedimiento de resolución es el siguiente:
Para empezar, podemos trazar una recta desde la bola blanca hacia un punto arbitrario de la zona central de la banda interna derecha, medir er ángulo entre el recorrido trazado y la superficie interna de la banda y, a continuación, trazar el recorrido de la bola refleja formando un mismo ángulo con la banda. Y es que según la ley de la reflexión, el ángulo de reflexión es igual al ángulo de incidencia.
Seguramente, la trayectoria que hemos trazado no llega a tocar la bola roja. Tenemos pues que cambiar la dirección del trayecto según el cual se dirige la bola blanca hacia la banda y trazar como antes la correspondiente trayectoria de la bola reflejada.
 |
| Fig 4 - Buscando el ángulo de tiro adecuado |
Tras variar de forma sistemática el ángulo de incidencia, podemos encontrar finalmente la dirección de tiro adecuada con la que la bola blanca alcanza, tras rebotar, el centro de la bola roja.
 |
| Fig. 5 - Ahora lo hemos encontrado. El recorrido de la bola blanca va hacia el centro de la bola roja. |
Pero esta solución no nos satisface. Lo que queríamos era encontrar la dirección de tiro correcta sin tener que ir probando. Nos falta indagar algo más y a ver si se nos ocurre algo mirando bien lo que tenemos hasta ahora....
Seguramente, además de la ley de la reflexión, hemos adquirido algunos conocimientos adicionales de óptica durante las lecciones de física de 1º o 2º de ESO y tal vez nos acordamos también de cómo se forman las imágenes en un espejo plano.
 |
| Fig. 6 - Formación de una imagen en un espejo plano |
Las figuras 5 y 6 parecen muy similares, sobre todo si prolongamos los recorridos divergentes de nuestra bola blanca en la figura 5 y situamos en el punto de convergencia de los recorridos una imagen de la bola blanca:
 |
| Fig. 7 - Prolongación hacia atrás de los recorridos divergentes e imágenes de las bolas al imaginar un espejo en lugar de la banda |
Este parecido no es de extrañar. Las dos figuras 5 y 6 son de hecho una ilustración de la ley de la reflexión. Además, el recorrido de una bola es también reversible (roja ha de golpear a blanca) y podemos por tanto imaginarnos también una imagen de la bola roja situada en el punto simétrico de la posición de la bola roja respecto de la banda.
Visto esto, podemos simplificar enormemente la búsqueda de la dirección de tiro adecuada. Lo único que tenemos que hacer es localizar (gráfica o mentalmente) la imagen especular de la bola roja y dirigir la bola blanca en dirección hacia esa imagen para conseguir golpear la bola roja. La siguiente figura lo ilustra en el caso de un tiro a una banda (caso 1):
 |
| Fig. 8 - Ilustración de la imagen de la bola roja que se obtendría al colocar un espejo y de la dirección del tiro a realizar (tras sacar el espejo) |
Caso 2:
Para encontrar la dirección de tiro adecuada para un tiro a dos bandas, tenemos que localizar la imagen de la imagen, es decir, la imagen formada por reflexión en la segunda banda de la primera imagen de la bola roja:
 |
| Fig. 9 - Ilustración de la imagen de la bola en el caso de dos espejos y trayectoria que debe realizar la bola blanca en el caso de un tiro a dos bandas |
 |
| Fig. 10 - Dibujo bidimensional de un tiro a dos bandas |
Esta representación rectilínea del recorrido de la bola en un espacio bidimensional formado por una red rectangular de imágenes especulares resulta también muy útil para analizar gráfica y visualmente las distintas opciones de juego que se tienen en una determinada distribución de las bolas. Esto se manifiesta claramente en el siguiente caso.
Caso 3:
Para determinar la dirección de tiro adecuada para un tiro a tres bandas, utilizaremos el mismo procedimiento gráfico de antes y obtenemos, al unir la posición de la bola blanca B con la de la imagen triplemente reflejada R''', la siguiente trayectoria que debe realizar la bola blanca para alcanzar el centro de la bola roja, en el caso de escoger la banda lateral derecha como primera pared de rebote:
 |
| Fig. 11 - Dibujo de un tiro a tres bandas en la red de imágenes especulares |
En el rectángulo verde, que representa el área de juego de la mesa de billar, puede verse la trayectoria real cuya imagen especular resultante de la reflexión en los tres espejos (bandas) es la línea recta entre B y R'''.
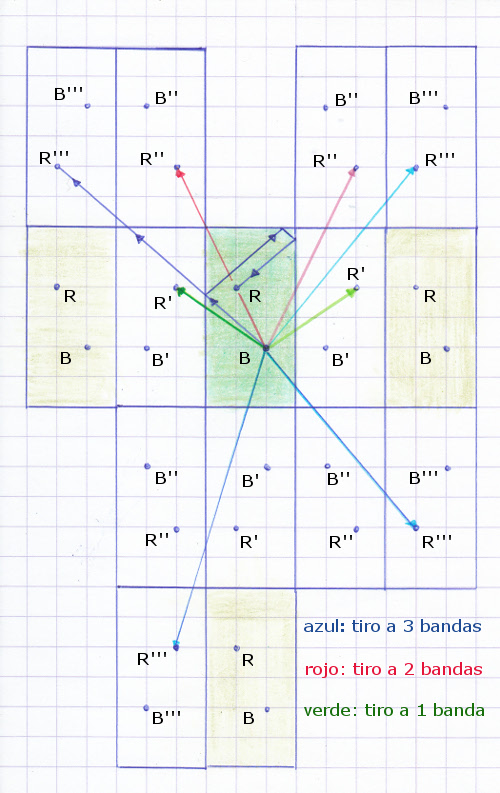
¿Pero es esta opción la mejor? ¿Podríamos alcanzar más fácilmente la bola roja mediante rebotes en otras tres bandas? Una representación de todas las posibles trayectorias que unen B con las distintas imágenes R''' que se obtienen en la red de imágenes especulares nos facilita la respuesta a estas preguntas.
 |
| Fig. 12 - Ilustración del recorrido de la bola en una vista reticular de imágenes especulares. Los recorridos en azul corresponden a las cuatro variantes de un tiro a 3 bandas, los recorridos en verde y en rojo, a tiros a una y dos bandas, respectivamente. |
La figura 12 nos permite ver qué variantes son más fáciles de realizar. Por ejemplo, en la disposición de bolas en la que nos hemos centrado, la opción de un tiro con rebote en la larga derecha (I) y luego en la corta superior (S) y larga derecha (D) (recorrido azul oscuro) es más difícil de realizar que la variante D-S-L (recorrido azul claro) debido a que es más fácil, en la primera opción, que se confundan las imágenes R''' y R' que uno solo ve mentalmente.
Los dos posibles recorridos a tres bandas que se dirigen hacia abajo (azul medio claro) son realizables en teoría, pero exigen una postura muy incómoda para el jugador que le impediría controlar bien el tiro y aplicar la fuerza requerida.
La figura 12 muestra asimismo que no puede realizarse un tiro a dos bandas I-O (recorrido rojo oscuro) debido a que requiere un ángulo de tiro que coincide, en la disposición de bolas considerada, con la de un tiro directo de la blanca contra la roja.
Todos estos ejemplos demuestran que un sentido espacial bien entrenado para la localización de imágenes especulares constituyen una guía útil para cualquier jugador de billar.
El procedimiento gráfico reticular es muy útil, pero no exacto. Si queremos determinar con exactitud el punto de impacto en una banda y el ángulo de tiro, tenemos que calcular la trayectoria de la bola. Esto lo haremos en la siguiente entrada de blog (entrenamiento B).
